파이썬 머신러닝ML
파이썬 경사하강법(Gradient Decent) 선형모델 기울기 구하기
양기호니
2022. 12. 8. 19:27
728x90
반응형
혼자 공부하려고 정리했어요~
경사하강법은 가설 h (hypothesis) = 가중치(W) * X
Cost함수 MSE(Mean Square Error, 평균 제곱 오차법)을 사용하여 최적의 기울기를 찾는 법 입니다.
Cost(W) = (1/n) * sum((H(X) - Y)^2)
W값을 0.6~3.5로 0.1 (leaning_rate) 간격으로 추정해서 cost를 구했습니다.
여기서 각 지점의 기울기를 구했는데요.
Cost(W)를 W로 미분하면
g (Gradient) = @Cost(W)/@W = (2/n)*sum((H(X) - Y)*X)
W_t+1 = W_t - g * (leaning_rate)
g가 0에 수렴할때까지 학습합니다.
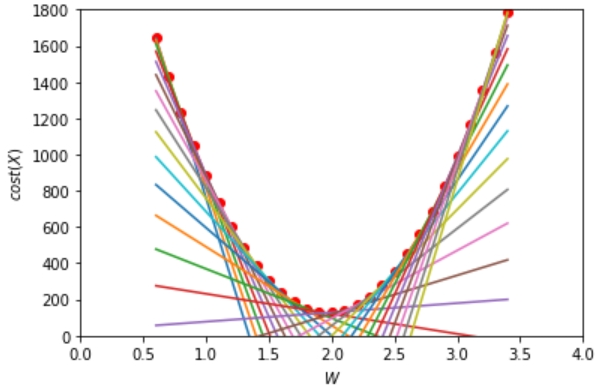
초기 학습되지 않았던 기울기에서 cost가 가장 낮은 지점을 찾아 기울기 값(W)를 찾아갑니다.

이런 복잡한 과정을 한방에 진행해주는 SGDRegressor 함수를 사용하시면 쉽게 기울기와 절편을 구할 수 있습니다.
from sklearn.linear_model import SGDRegressor
np.random.seed(0)
n = 30 #sample count
X = np.arange(n, dtype=np.float32).reshape(-1,1)
y = X * 2 # W = 2, b=0(bias 생략)
y = y + 11 * np.random.randn(n,1) # adding noise
plt.plot(X, y, 'b.')
lr = SGDRegressor(learning_rate='constant', eta0=0.001) #constant로 입력시 eta0의 값이 들어감
lr.fit(X, y.ravel())
W = lr.coef_
b = lr.intercept_
print('W:', W, 'b:', b)
plt.plot(X, W.ravel()*X + b, 'r-')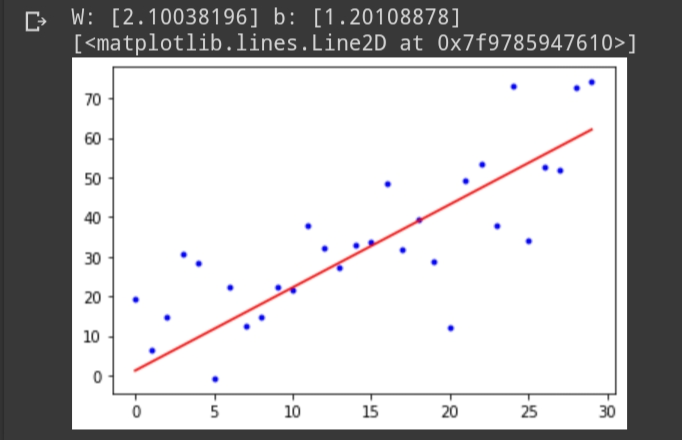
반응형